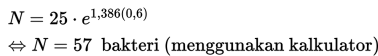FUNGSI EKSPONEN DAN PENERAPANNYA
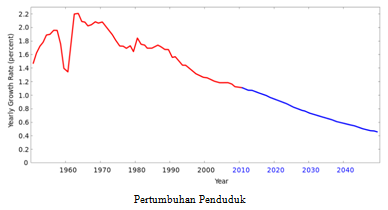
Pernahkah kamu mendengar tentang peramalan jumlah penduduk di masa yang akan datang? Dalam merencanakan pembangunan jangka panjang di berbagai bidang, pemerintah perlu meramalkan jumlah penduduk beberapa tahun ke depan untuk menjamin peningkatan pertumbuhan ekonomi, ketersediaan sumber daya alam dan fasilitas umum.
Kamu telah belajar mengenai eksponen/bentuk pangkat di kelas X. Apakah kamu masih ingat? Mari kita ingat kembali mengenai eksponen.
Definisi Bilangan Berpangkat Bulat Positif
Untuk a bilangan real dan n bilangan bulat positif berlaku
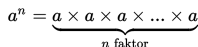
Sifat-Sifat Eksponen
Jika a dan b adalah bilangan real tak nol, sedangkan p dan q adalah bilangan rasional, maka berlaku hubungan sebagai berikut :
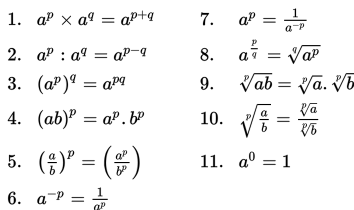
Lalu, apa perbedaan antara fungsi eksponen dengan eksponen/bentuk pangkat? Fungsi eksponen merupakan bentuk perpangkatan yang pangkatnya merupakan suatu fungsi, sedangkan eksponen pangkatnya adalah bilangan rasional. Mari pelajari lebih lanjut tentang fungsi eksponen.
Definisi Fungsi Eksponen
Agar kamu lebih paham cara membedakan fungsi yang termasuk fungsi eksponen, perhatikan beberapa fungsi berikut.
f (x) = 8 x (fungsi eksponen)
f (x) = x 8 (bukan fungsi eksponen)
f (x) = (12)x (fungsi eksponen)
Sifat-Sifat Fungsi Eksponen
• Diketahui fungsi eksponen y = f (x) = kax, maka domainnya (daerah asalnya) adalah himpunan seluruh bilangan nyata, Df = {x | x ϵ Ɍ}.
• Daerah hasilnya (rangenya) adalah himpunan seluruh bilangan nyata (real) positif, Rf = {y | y > 0, y ϵ Ɍ}.
• Grafik fungsinya selalu memotong sumbu y di titik (0, 1).
• Fungsi f (x) = ax merupakan fungsi naik untuk a > 1 dan merupakan fungsi turun untuk 0 < a < 1, serta merupakan fungsi konstan untuk a = 1.
• Grafik fungsi tidak bisa memotong sumbu x . Sumbu x merupakan asimtot datar.
Bentuk-Bentuk Fungsi Eksponen
• Berbentuk f (x) = a x dengan a > 1, a ϵ Ɍ dan x ϵ Ɍ.
Fungsi Eksponen f (x) = a x untuk a > 1 disebut sebagai fungsi monoton naik, sebab jika x1 < x2maka ax1 < ax2.
Bentuk di atas dapat dinyatakan dalam pertidaksamaan yang lebih umum, sebagai berikut:
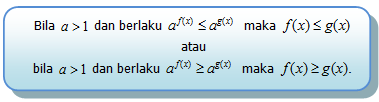
Fungsi Eksponen f (x) = a x untuk 0 < a < 1 disebut sebagai fungsi monoton turun, sebab jika x1> x2 maka ax1 > ax2.
Bentuk di atas dapat dinyatakan dalam pertidaksamaan yang lebih umum, sebagai berikut:
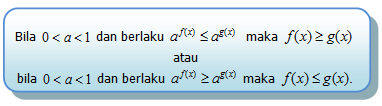
Penerapan Fungsi Eksponen
y = b. a x dengan a = 1 + r
Keterangan:
b = jumlah awal (ketika x = 0)
a = faktor pertumbuhan (a > 1)
r = laju pertumbuhan per selang waktu T.
y = jumlah setelah selang waktu t
x = fraksi dengan x = tT
• Fungsi Penyusutan Eksponensial
y = b. a x dengan a = 1 – r
Keterangan:
b = jumlah awal (ketika x = 0)
a = faktor penyusutan (0 < a < 1)
r = laju penyusutan per selang waktu T.
y = jumlah setelah selang waktu t
x = fraksi dengan x = tT
• Fungsi Peluruhan Radioaktif
m = m0 × (12)n
Keterangan:
m = massa setelah selang waktu t.
m0 = massa awal
n = tT
t = selang waktu
T = waktu paruh
Mari kita cermati beberapa contoh soal berikut ini.
Contoh 1
• P = ( 2, 14)
• Q = (3, 8)
Penyelesaian:
• P = ( 2, 14)
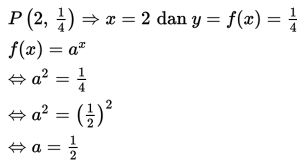
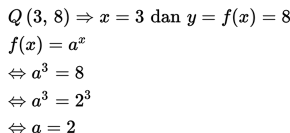
Contoh 2
• Tulis persamaan untuk memodelkan jumlah penduduk Indonesia.
• Tentukan jumlah penduduk Indonesia pada tahun 2020.
Penyelesaian:
• Model jumlah penduduk Indonesia.
Oleh karena laju pertumbuhan penduduk = 2% pertahun artinya jumlah penduduk selalu meningkat, maka gunakan fungsi pertumbuhan eksponensial, yaitu:
y = b. a x dengan a = 1 + r
Misal:
b = jumlah penduduk pada tahun 2010 = 230.000.000
r = laju pertumbuhan pertahun = 2% = 0,02
a = faktor pertumbuhan = 1 + r = 1 + 0,02 = 1,02.
Dengan demikian, jumlah penduduk Indonesia bisa dimodelkan sebagai:
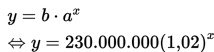
t = lama waktu pertumbuhan = 2020 – 2010 = 10 tahun
T = selang waktu pertumbuhan = 1 tahun
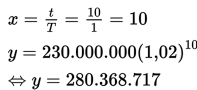
Contoh 3
• 0,6 jam
• 3,5 jam
Penyelesaian:
Substitusikan, N0 = 25 ke persamaan, maka diperoleh
N = 25. e1,386t
• Nilai N ketika t = 0,6